Binary Scopes

By: David Williamson

---

This excercise will cover:

• functions
• scope
• algorithmic complexity

---

Materials:

• small whiteboards & dry erase markers (x2)
• ten-sided die, or 'd10'
• calculator
• pen and paper

Procedure:

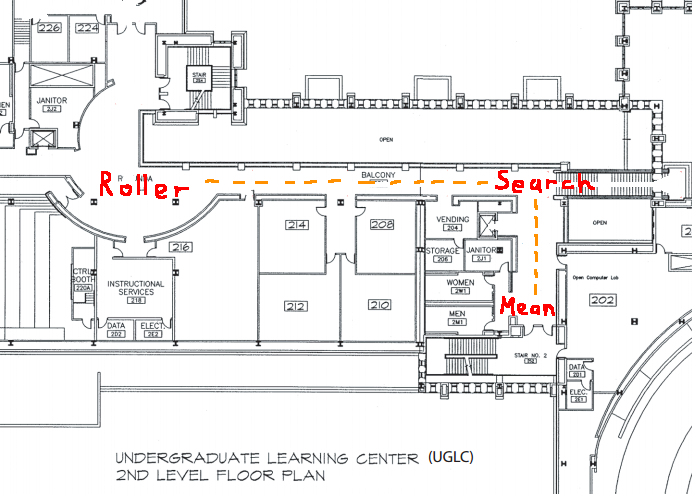
The students are separated into three groups:

• Roller
• Search
• Mean

The Search group will be relaying communications between the Roller and Mean groups, in order to determine the number rolled by the Roller group. They will do this by making use of the binary search algorithm. The groups will be separated by a large distance, in the UGLC, such that they will have to write their communications in large letters on white boards.

The Roller group will be in charge of generating a randon number, using a ten-sided die. They will also read guesses from the Search and respond if the guess is successful, or whether it is to high or too low.

The Search party will then adjust their high and low bounds, so for instance, in the beginning, if the number of rolls the Roller group makes is 2, the lower bound will be 0 and the upper bound will be 99. The first thing they do is report these bounds to the Mean group, which responds with the arithmetic floor-mean of the bounds, which is 50 in this case. So the Search group passes the guess to the Roller group. Assuming the number was something like thirty, the Roller group would respond by saying the guess was too high, so the Search group would make 50 the new upper bound and ask the Mean group for the average of 1 and 50, and the new guess would be 25, and so on.

---

Here is the algorithm implemented in Python:

from random import randint

# The function of the Roller is generating a number, and comparing guesses to it.
class Roller():
    def __init__(self, rolls=1, sides=10, number=None):
        self.size = sides**rolls
        if number == None:
            self.number = randint(0, self.size - 1)
        else:
            self.number = number
    def check(self, guess):
        if guess == self.number:
            return 'success'
        elif guess > self.number:
            return 'high'
        else:
            return 'low'

# The Mean generates the average between low and high bounds, to find the next guess.
mean = lambda s: int(sum(s)/len(s))


# The Search communicates between the two other groups, adjusting high and low bounds,
# depending on responses from the Roller group.
# This group also recores the number of guesses. 
def search(roller):
    low, high, tries = 0, roller.size - 1, 1
    guess = mean((low, high))
    while roller.check(guess) != 'success':
        tries += 1
        if roller.check(guess) == 'low':
            low = guess
            if high - low > 1:
                guess = mean((high, low))
            else:
                guess = high
        if roller.check(guess) == 'high':
            high = guess
            guess = mean((low, high))
    return tries
        

def binaries(rolls):
    step_list = []
    for i in range(10**rolls):
        step_list.append(search(Roller(rolls=rolls, number=i)))
    return step_list

binaries(1)

[4, 3, 2, 3, 1, 2, 2, 3, 4, 5]

def ranges(pows, collector):
    collection = []
    for i in range(pows):
        collection.append(collector(binaries(i + 1)))
    return collection 

ranges(4, max)

[5, 8, 11, 15]

ranges(4, mean)

[2, 4, 7, 9]